요즘에는 공부가 지루하면
알고리즘 문제를 풀곤한다.
오늘 푼 문제는 드래곤~! 커~~브~~~!
https://www.acmicpc.net/problem/15685
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커
www.acmicpc.net
나는 어떻게 풀었을까?
비효율적인 알고리즘
내가 처음 생각했던 건 아래와 같다.

0세대를 먼저 배열에 표기하고,
0세대를 복제하여, 90도 회전한 배열이 있다.
원본과 복제본의 각 끝점의 좌표를 기억해둔다.
원본의 끝점과 복제본의 끝점 좌표를 뺴주어 변화량을 알아낸다.

복제본의 값들을 변화량 만큼 x, y좌표를 이동시켜 준다.
이동을 완료한 복제본을 원본에 더해준다.
해당 행위를 반복한다.
이런 방식은 답은 도출하겠지만,
90도 뒤집기 위한 2중포문
이동하기 위한 2중포문과 임시 배열
붙여넣기 위한 2중포문
까지 상당히 비효율적인 행위를 반복하게 된다.
문제의 배열 크기가 작아 통과는 하겠지만,
좋은 방안이라 생각되지 않는다.
비교적 효율적인 알고리즘
알고리즘 그림 그리다가 우연히 규칙을 발견했다.
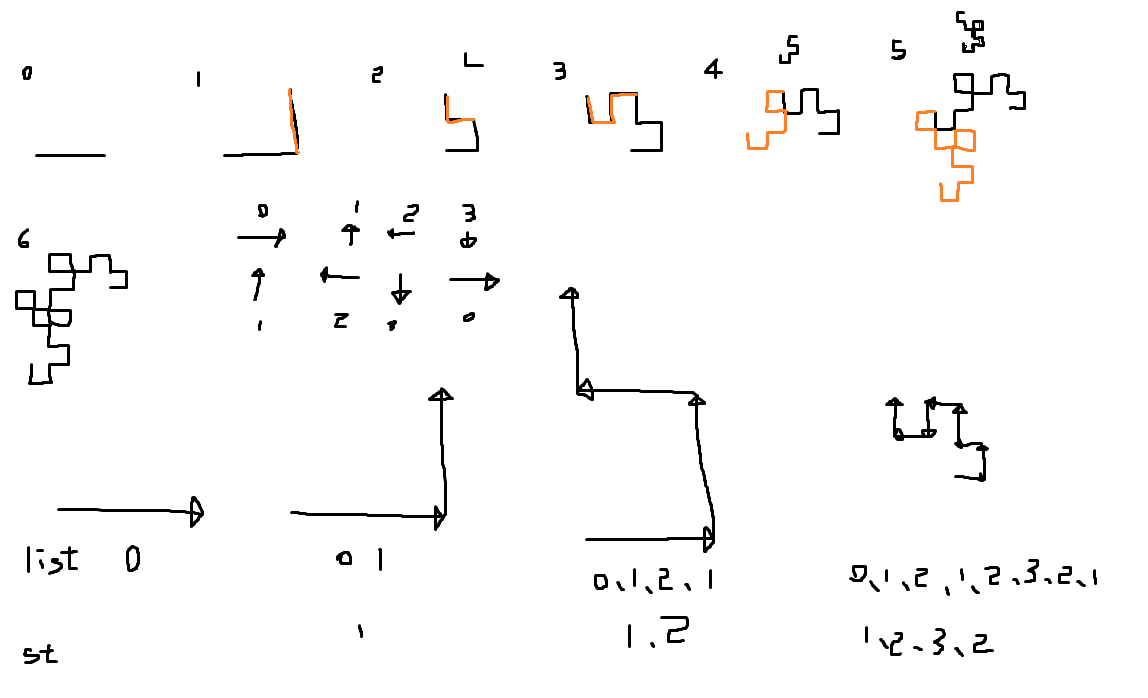
핵심은
끝점을 기준으로 어느 방향을 가르키는가?!

위 사진을 보면 0세대, 0세대의 회전, 1세대의 모습을 볼 수 있다.
0세대를 회전한 결과 끝점의 방향은 아래방향이지만,
1세대를 보면 진행이 위로 되기 때문에, 끝점의 방향 또한 위로 향한다.
호오옹 신기하당
여러 세대로 한 번 확인할까?

여러 세대를 보니 또다른 규칙이 보인다...!
회전 방향이 아래라면, 실제 진행은 위
회전 방향이 위라면, 실제 진행은 아래
회전 방향이 왼쪽이라면, 실제 진행은 오른쪽
회전 방향이 오른쪽이라면, 실제 진행은 왼쪽
이걸 번호로 나타내면 이렇게 보인다.

뭐야! 그럼 이렇게 하면 구해지겠네??
(원래 방향 +1) % 4
여기서 떙큐 하고 나가면 안된다.

2세대의 방향이 [0, 1]일 때,
규칙을 통한 방향변환의 결과는 [1, 2]이다.
얏호 그럼 [0, 1, 1, 2]를 실행하자! 라고 하면 주황색 선의 결과가 나온다.

우리는 변환한 순서를 뒤집어 준 뒤에야 원하는 결과를 얻을 수 있다!!
나는 이 순서를 뒤집기 위해 스택을 이용했다.

입력 리스트, 즉 이전 세대의 방향이 기록된 리스트에서
값을 하나씩 변환하여 스택에 넣는다.

모두 변환했다면 하나씩 다시 담아준다.
그렇다면, 변환과 뒤집기 완료!!
여기까지가 이렇게 나타난다!!
// 이동 지점을 표시하는 2차원 배열
int grid[105][105];
void draw(int x, int y, int d, int g) {
// 변환 방향
int convert[] = { 1, 2, 3, 0 };
// 각 방향에 따른 이동 좌표
int cnvtX[] = { 1, 0, -1, 0 };
int cnvtY[] = { 0, -1, 0, 1 };
stack<int> dir; // 값을 뒤집기 위한 스택
vector<int> list; // 모든 방향을 담든 벡터
list.push_back(d); // 0세대는 미리 넣는다.
// 모든 세대를 돌 때까지
for (int i = 0; i < g; i++) {
// 리스트의 값을 변환하여 스택에 넣고
for (int j = 0; j < list.size(); j++) {
dir.push(convert[list[j]]);
}
int size = dir.size();
// 변환된 값을 스택에서 꺼내어 집어넣는다.
for (int j = 0; j < size; j++) {
list.push_back(dir.top());
dir.pop();
}
}
// 시작지점 표기
int sX = x, sY = y;
// 시작점은 미리 표기
grid[sY][sX] = 1;
// 리스트에 표기된 모든 방향을 돌 때까지
for (int i = 0; i < list.size(); i++) {
// 정의된 방향 좌표로 이동하여
int plusX = cnvtX[list[i]];
int plusY = cnvtY[list[i]];
sX += plusX;
sY += plusY;
// 표시한다.
grid[sY][sX] = 1;
}
}
사각형 개수 탐색은 간단하게,
네 꼭지점 모두 탐색흔적이 남았다면 카운팅 했다.
int calRect() {
int cal = 0;
// 최대 크기가 100이라서 100개 탐색
for (int i = 0; i < 100; i++) {
for (int j = 0; j < 100; j++) {
// 네 꼭지점이 모두 탐색되었다면 카운팅 증가
if (grid[i][j] && grid[i][j + 1] && grid[i + 1][j + 1] && grid[i + 1][j]) {
cal++;
}
}
}
return cal;
}
전체코드는 아래와 같다.
#include <vector>
#include <iostream>
#include <string>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <list>
using namespace std;
// 이동 지점을 표시하는 2차원 배열
int grid[105][105];
void draw(int x, int y, int d, int g) {
// 변환 방향
int convert[] = { 1, 2, 3, 0 };
// 각 방향에 따른 이동 좌표
int cnvtX[] = { 1, 0, -1, 0 };
int cnvtY[] = { 0, -1, 0, 1 };
stack<int> dir; // 값을 뒤집기 위한 스택
vector<int> list; // 모든 방향을 담든 벡터
list.push_back(d); // 0세대는 미리 넣는다.
// 모든 세대를 돌 때까지
for (int i = 0; i < g; i++) {
// 리스트의 값을 변환하여 스택에 넣고
for (int j = 0; j < list.size(); j++) {
dir.push(convert[list[j]]);
}
int size = dir.size();
// 변환된 값을 스택에서 꺼내어 집어넣는다.
for (int j = 0; j < size; j++) {
list.push_back(dir.top());
dir.pop();
}
}
// 시작지점 표기
int sX = x, sY = y;
// 시작점은 미리 표기
grid[sY][sX] = 1;
// 리스트에 표기된 모든 방향을 돌 때까지
for (int i = 0; i < list.size(); i++) {
// 정의된 방향 좌표로 이동하여
int plusX = cnvtX[list[i]];
int plusY = cnvtY[list[i]];
sX += plusX;
sY += plusY;
// 표시한다.
grid[sY][sX] = 1;
}
}
int calRect() {
int cal = 0;
// 최대 크기가 100이라서 100개 탐색
for (int i = 0; i < 100; i++) {
for (int j = 0; j < 100; j++) {
// 네 꼭지점이 모두 탐색되었다면 카운팅 증가
if (grid[i][j] && grid[i][j + 1] && grid[i + 1][j + 1] && grid[i + 1][j]) {
cal++;
}
}
}
return cal;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int x, y, d, g;
cin >> x >> y >> d >> g;
draw(x, y, d, g);
/*for (int j = 0; j < 100; j++) {
for (int k = 0; k < 100; k++) {
cout << grid[j][k] << " ";
}
cout << endl;
}*/
}
cout << calRect();
}
'심심풀이 알고리즘 > 백준' 카테고리의 다른 글
| [백준] IF문 좀 대신 써줘 19637번 - (C++ 20, C++ 23) (0) | 2025.01.02 |
|---|---|
| [백준] 로봇 청소기 14503번 - (Java) (0) | 2023.08.25 |
| [백준] 16197번 두 동전 - (JAVA) (0) | 2023.08.20 |
| [백준] 15686번 치킨 배달 - (JAVA) (0) | 2023.08.11 |
 메프도의 요약노트
메프도의 요약노트




댓글